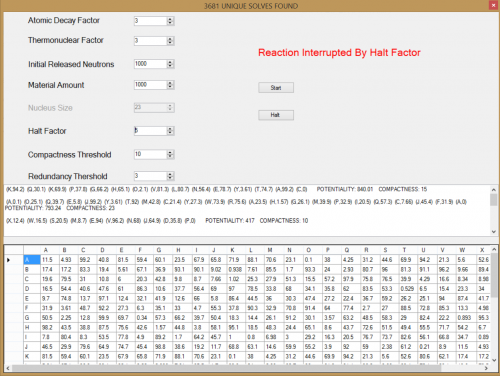
Introduction:
This is the first generation of very new algorithms; we are going to project a famous phenomenon in nuclear physics called Nuclear Fission onto optimization problem.
Basic Definitions:
Nuclear Fission:
When a neutron strikes the nucleus of an atom of the isotopes uranium 235, it causes that nucleus to split into two fragments, each of which is a nucleus with about half the protons and neutrons of the original nucleus. In the process of splitting, a great amount of thermal energy, as well as gamma rays and two or more neutrons, is released. Under certain conditions, the escaping neutrons strike and thus fission more of the surrounding uranium nuclei, which then emit more neutrons that split still more nuclei. This series of rapidly multiplying fissions culminates in a chain reaction in which nearly all the fissionable material is consumed.
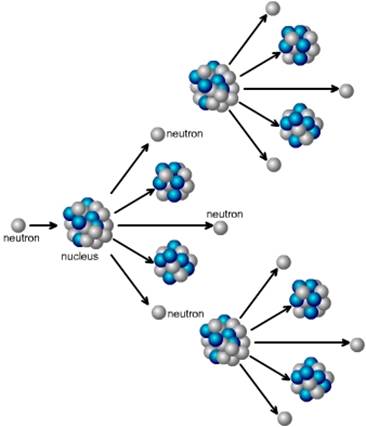
Neutron & Proton:
Neutron: elementary particle in atomic nuclei which has no electrical charge , we will represent it as a { name , value} , in our proposed example: the name will be an alphabetic letter and the value will refer to the sub-weight between the current neutron and the next neutron.
Proton: elementary particle with a positive electrical charge , we will represent it
as a { name , value} , in our proposed example: the name will be [PROTON] always and
the value will be discarded because we ignore electric effect here .
the reason why we use protons will be mentioned later.
Nucleus:
Organized group of Neutrons and Protons (because order matters in our example) .
Compactness:
It describes nucleus inner structure , here it is defined as the total number of neutrons inside the nucleus.
Redundancy:
It describes nucleus inner structure too, and it is defined as the biggest frequency of all
neutrons inside the nucleus . of course it can’t be less than one.
Potentiality :
Latent power of the nucleus , it describes its ability to be a best solve (when maximized or minimized) . it is implemented for every nucleus by the sum of all neutrons’ weights in the nucleus.
We will be looking for the optimum nucleus with the lowest potentiality (for a minimization problem example) that satisfies compactness and redundancy terms .
Criticality:
Criticality state (of entire reaction) is determined by the probability that a neutron released in fission will cause a subsequent fission .If on the average less than one neutron causes another fission, the rate of fission will decrease with time and ultimately drop to zero. This situation is called subcritical. When more than one neutron causes a subsequent fission, fission rate and power increase and the situation is termed supercritical.
Thermonuclear Factor :
The stronger the explosion the more thermal energy will be produced , more heat (bigger explosion) will arise when more neutrons are released after each single split (this will enhance reaction’s criticality), it is characterized here by the average number of released neutrons.
Atomic Decay Factor :
After split the unstable atomic nucleus decays into a more stable nucleus emitting beta particles and gamma rays.
In negative beta decay (symbolized β−-decay) an unstable nucleus emits an energetic electron and an antineutrino, and a neutron in the nucleus becomes a proton that remains in the product nucleus.
Here we neglected electron and antineutrino effects to keep things simple.
We will choose the worst neutron of the nucleus for that decay.
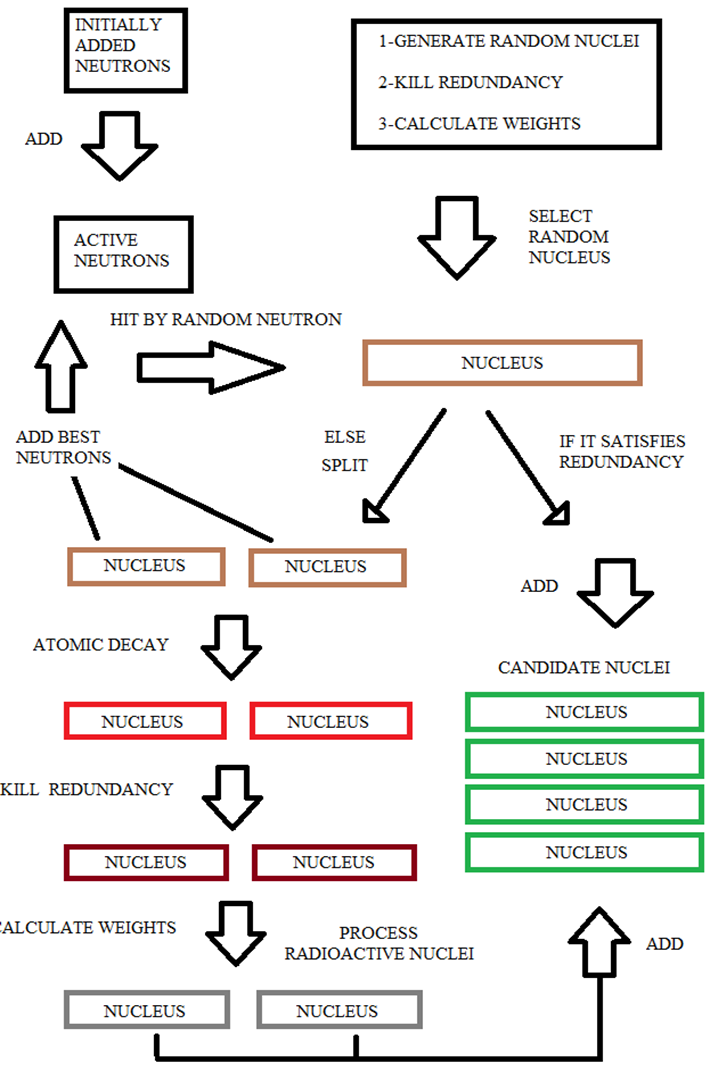
Next diagram will help clarify the fundamentals of this algorithms :
 Data Structures and Implementation:
Data Structures and Implementation:
We will try to take the simplest way to implement our concepts; otherwise calculations will get so complex .
Class Simulation_Problem :
The problem is simulated by a 2D array representing the costs of travelling from state
X1 to state X2.
States are named as alphabetical letters {A . . Z}
This class is generated each time you load the application to create a new random matrix of real numbers.
To get the cost [X1 - X2] we will look to the X1 row and the X2 column in the matrix.
Class Neutron :
(name as string , value as double)
This will be used for both neutrons and protons , but when it is used for protons the name
will be “PROTON” ,when it is used for neutrons the name will be an alphabetical letter.
Class Nucleus :
-Sub Random_Fill_Nucleus(): to fill it with random neutrons and protons after each reaction.
-Function Potentiality(): To get the sum of weights in the nucleus we want to minimize it
to reach the lowest possible cost and this is what the reaction will do.
-Function Redundancy():will look for the maximum repetition in the nucleus , it is a harsh term where many solves will be excluded because of it as we will see later, it can’t be less than one.
-Function Compactness(): how many neutrons we got in the nucleus , this will be a significant condition in the optimal solve where we are obligated by a minimum value of this, there is no one certain answer for this problem so we will generate solves above certain threshold of compactness and will leave it to the end user to determine his finest answer.
-Sub Emit_Beta(): will look for the neutron of the worst value in the nucleus and
turn it into a proton.
Class Serial_Reaction:
-Sub initialize(): for all material amount: generate a random nucleus with no redundancy (redundancy= 1) and calculate the weights of all random nuclei .
we also have a set of active neutrons and we will fill it by an initially released neutrons
determined by the user (which is a number of random neutrons ) , sure this will affect escalation of nuclear reaction.
If we didn't assign any value to best solve before then assign any nucleus to it.
(This will happen just only before first reaction).
-Sub Release(): It applies a series of reactions to the material and it is illustrated by these steps:
Check Halt Factor to see if we should stop mandatorily
For each nucleus in the material:
-Get a random neutron of the active neutrons set.
-Generate a suitable random integer to determine hit place
-Insert the active neutron inside the nucleus to implement the hit
-If the hit nucleus satisfies redundancy and compactness thresholds, it will not be
sacrificed.
but it will be marked as “not ready” to continue the reaction and it will be
added to candidates list.
-If the hit nucleus does not satisfy thresholds , it will suffer a nuclear fission :
+ Split the nucleus into two equal parts.
+ In each part seek the neutron of the best value (lowest value).
+ Add best found neutrons to active neutrons list with respect to thermonuclear factor
+ The both parts then will suffer atomic decay with respect to atomic decay factor.
+ Process radioactive nuclei after atomic decay
(remove invalid redundancy and recalculate values for both parts because the
nucleus structure is changed)
and add them after that to candidates list too.
Probe the new candidates list : If we find a nucleus with a better overall cost
(lower potentiality) then this is our new best solve.
Call Sub initialize() to prepare for a new reaction.
Using the Program:
[Please read the whole article before you run the program]
Actually the Program will make most of the work for you, it will generate a new problem
every start , you just want to set the suitable parameters for the algorithm.
Don’t use a massive material amount or big atomic decay factor (we will get to that)
massive material amount or huge nucleus size will cause your computer to hang-up.
(I use core2dou with 4GB Ram computer for the default Parameters)
Halt factor will determine number of reactions , and because we used letters A..Z
as possible states then compactness can’t exceed 26 (interface will protect most of
sensitive parameters) .
Press Start to begin , if it takes so long then press Halt and change the parameters
to study their effect.
(you might need to implement new problem in the code to study the effect well)
in the upper caption of the form you will see number of unique solves
(repeated solves will be excluded from this) and optimal solves will be printed in
the text box in the middle of the form.
Points of interest:
We found that the optimum nucleus size for many examples can be estimated by this equation:
nucleus size = compactness factor * 2 + redundancy factor
Therefore it is automatically set by the program.
If you study the code in depth you will realize that each reaction’s state will be supercritical at start. and after time it will turn into subcritical. This is good because we are not sure of the perfect value of compactness and this way will give us a good rang of compactness because of splitting.
Sometimes if you change the parameters you will see that after a while the reaction’s state will be subcritical and then all fissionable material will be consumed therefore the serial reaction will fail to continue , you should try to avoid going through this case.
Here we implemented To-String() sub to display only Neutrons, actually if you display the
whole nucleus you will (sometimes) see Protons in it , in our implementation we bypassed these protons because we assumed that their occurrence or its order does not affect weights calculations.
In real world the released neutrons after split will be two or more , so choose
a suitable number (bigger than one of course) as a thermonuclear factor to maintain
supercritical state and to avoid going into situation “Fissionable Material Is Consumed”.
Because of the nature of atomic decay mechanism , the compactness will be deeply
influenced by atomic decay factor , therefore you should choose a relatively small number (but bigger than zero).
Nuclei will have a big potentiality at start where the reaction will be supercritical and because of splitting (which will reduce compactness and therefore total neutrons cost) nuclei will have a small potentiality where the reaction will turn into subcritical and this is what we want because active neutrons will hit small potentiality nuclei to produce more new optimal solves.
Function Redundancy_Killer() is very important to reduce redundancy to minimum level (1)
so we can generate new random comparable nuclei.
Nuclei were initialized with 10% protons in this example.
Real World Application(Example):
An airlines company wants a work plan to organize its flights across many countries , to visit
at least X airports with lowest amount of fuel , and with a condition like : must not visit the same airport more than (N times) 3 or 4 times ..because passengers will not be much and so the economic income will not be optimal.
This is a nuclear algorithm where :
Neutron : airport
Nucleus: work plan
Compactness is : X
Redundancy is : N
Potentiality is : total cost of traveling across airports (in any nucleus)
Other factors are experimental and set by user to reach best answer.
Nuclear vs. Genetic algorithms (Why Nuclear is better?):
Genetic algorithms (unlike here) will not directly exclude a bad gene from a candidate
solve. instead of that it will require many generations (of mutation and crossover).
In genetic algorithms the genome length is fixed unlike nuclear algorithms which can be used to solve problems where solve length is unknown.
Genetic algorithms do not identify the sub-solve ‘Unknown ' or ‘Dead End’
while it is identified here (Proton) .
Nuclear Algorithms will converge much more faster than genetic algorithms
because of atomic decay.
Genetic algorithm does not deal with a hard condition like maximum allowed repetition
of certain genes in the chromosome, and if you try to implement this you will
realize later that this condition will make genetic algorithm converge (much slower).
Genetic algorithms are so influenced by the past generation which could be bad
but nuclear algorithms start randomly after each reaction therefore there is a better
chance to find a new undiscovered better solve (as a totally new breed in GA)
after past reaction.
Genetic algorithms talk about blind (unstudied) mutations and don’t use any function to
find the “Best Mutation” unlike nuclear algorithms which utilize “Neutrons of best weights”
to perform nuclear fission (this is like to apply mutations of best likelihood to produce best
possible genome in GA).